Time Warp: Delayed-Choice Quantum Erasure . . .

Can photons ‘reach back in time’??

Like most of my posts, this one is free and reasonably non-technical; my few premium posts have technical content. (Audio version below.)

I considered sending this post back in time to make up for the major delay in publishing it – but I hope that readers with a fair degree of foresight will have looked ahead and seen that it was going to be worth waiting for.

This is quite a long read – but its implications are rather important. So I hope you’ll stick with it.

To hear an audio version of this post (45 mins), click the arrow below:

Just a reminder: To see a full list of posts in sequential order, with a brief summary of each, go to https://ihs.ac/s.php .

Background

In 1801 Thomas Young changed the course of science forever, by the simple act of shining a light through two closely-spaced slits in a card onto a screen beyond. In this one apparently trivial step he established that light travels in a wave: on recombining, the two beams of light from the two slits formed an interference pattern on the screen, a pattern of light and dark stripes resulting from the peaks and troughs of the wave from one beam alternately adding to and cancelling out the peaks and troughs from the other beam. This was arguably the first step ushering in the science of Quantum Mechanics, illustrating as it did: (a) the wavelike nature of light (to be followed some time later by a similar observation relating to particles of matter); and (b) the probabilistic nature of outcomes of physical events at a subatomic level.

When, in due time, it was found that light is made up of discrete packets, or quanta, of energy – now known as photons – there was of course some interest in trying to identify which of the two slits any particular photon had passed through. This again pushed science further forward – basically by adding two rather puzzling features to the story. First, when any sort of mechanism was set up to detect photons going through one slot or the other, the interference pattern disappeared. Second, a more advanced version of the experiment still built up the same sort of interference pattern when individual photons were fired sequentially at the double-slit card – indicating without doubt that each individual photon was subject to self-interference as its split waveform recombined on the other side of the card and landed on the screen. [Astute readers will realise that this was in fact apparent from Young’s original experiment (with hindsight, since the quanta of energy now referred to as photons were not known of in Young’s time): Young’s light beam was neither coherent nor monochromatic, so the likelihood of two or more photons interacting to contribute to a consistent interference pattern – or any pattern at all – was effectively zero; that pattern observed by Young (and many others) had to be from each individual photon interfering with itself.]

Stepping Up The Game With Quantum Entanglement

For some time it was believed that any mechanism used to detect the passage of a photon through one or other slit was disrupting the superposition (composite form) of the waves through the two slits, destroying the interference pattern – the well- known ‘observer effect’ that modifies outcomes at a quantum level. Then came the use of quantum entanglement, to separate the acts of which-path detection and interference-pattern formation. After passing through the double-slit, each photon is ‘frequency-halved’ (Down-conversion) into two entangled photons each carrying half the energy of the original. These entangled photons are effectively linked: whatever happens to one, the corresponding thing happens to the other. The output for any one photon from each slit (let’s call them L & R, for left and right slit) will then become L & R components in each of the two entangled photons resulting from that single photon passed through the slits. So we can test one to see which slot it went through and leave the other untouched to make an interference pattern – can’t we?

This is achieved by leading the outputs (L & R) from the two slits in different directions, then down-converting each of those two outputs to give corresponding L & R components for each of the (now) two entangled photons which each carry half the energy of the original photon; this entanglement ensures that the fates of those two lower-frequency photons are inextricably linked: whatever happens to one determines what happens to the other.

For one of these (the signal photon), L & R components are brought back together – effectively as they would normally be in the original Young’s experiment – to land on a screen. So far so good: all else being equal we would expect a collection of such photons to form an interference pattern, much as seen by Young (and countless others after him). But here’s where the plot thickens: the L & R components of the other entangled photon (the idler photon) are led to separate detectors, where each photon will register on either the L detector or the R detector – giving irrefutable evidence of which slit that photon, and so also its entangled twin, must have passed through.

We Can’t Have It Both Ways – Can We?

So, we have a paradox: an interference pattern can only occur when the waves of the original photon pass through both slits, giving L & R wave components which can interfere with each other. That’s not a problem for the signal photon, whose wave patterns from L & R slits have been brought back together; but it is a problem for the idler photon, which is forced to divulge which one of the two slots it came through – and it must be just one of the two slots, since one photon cannot register in two places. The astounding – but also totally inevitable – outcome is that this forced single-slot-selection of an idler photon also forces single-slot-selection by its entangled signal-photon twin – not detected directly but very evident from the pattern made by those signal photons on their detector screen: no interference pattern appears on that screen. In other words, simply observing (or even just making potentially observable) the path taken by one photon alters the behaviour of its entangled twin.

Just to add to the mystery, if the L & R outputs for the idler photon are brought back together without first recording L-or-R information on separate detectors – an interference pattern then appears on the screen showing signal photon outcomes! In other words, obliterating which-path info for the idler photons removes the which-path info acted on by the signal photons – so they can receive info from both slits and thus create an interference pattern!

[All of these situations/setups are illustrated in the diagram below of the experiment of Kim et al.]

This has led to a rather astounding conclusion based on the wave-particle duality of light – i.e. the fact that light can apparently exist either as a wave or a particle, but not both at once. That conclusion is that, just by making the behaviour of a photon observable, by whatever means, that photon is forced to change its behaviour from that of a wave (i.e. distributed) to that of a particle (i.e. following a single narrow path). More than this, detection of photon behaviour well after it passes through one or both slots causes that photon to change its behaviour at the time of encountering the two slots – i.e. retrospectively.

Those Darned Time-Travelling Photons!

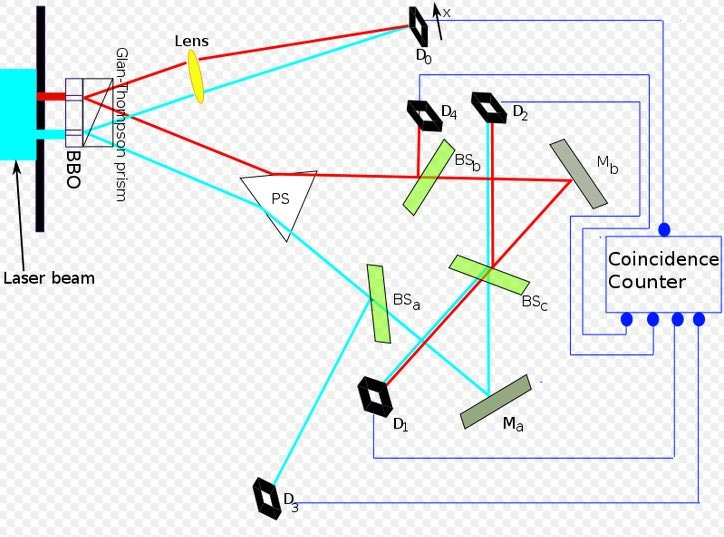
Not surprisingly this has led to intense interest in the apparent ability of photons to reach back in time to alter their past behaviour as a result of future circumstances. The practical outworkings of this interest are well demonstrated by the experiment of Kim et al in 1999 (Phys. Rev. Lett. 84(1), pub. Jan 2000). A schematic of the experimental setup is shown below [author: P E Moran; reproduced under the terms of the GNU Free Documentation License].

A sequence of photons from a laser source is passed through a double-slit arrangement. The outputs from the two slits, which together comprise the energy of a single photon at a time, are separated (red (R) and blue (B) lines); each output is then frequency-halved (down-conversion) to give the two ‘slit components’ (R & B) of each of two entangled photons, the ‘signal’ photon and the ‘idler’ photon. The R&B components of the signal photon are re-combined and led upwards, ultimately to a detector Do which is able to track the ‘landing’ position of that photon; the R&B components of the entangled idler photon are sent in widely differing directions and each then directed to a sequence of mirrors and beam-splitters. Here each (R & B) is first split by a 50/50 beamsplitter (BSa, BSb); in each case one of those 50% R or B parts is directed straight towards a detector (D3, D4); the other 50% R or B part (after being reflected off a mirror, Ma or Mb) is passed through a third 50/50 beam-splitter (BSc) which combines those two remaining R & B parts, at the same time splitting that R&B mix into two parts each consisting of 50/50 R & B components, identical except for the fact that R&B are in phase in one mix & out of phase in the other (due to phase shifts at the various mirrors & beamsplitters). Those two 50/50 R&B pairs of components are then directed to two detectors, D1 and D2. This is all hopefully clear from the diagram above.

Here’s where it gets interesting. Each signal photon reaches detector Do around 8 nanoseconds before its idler-photon entangled twin reaches one of the detectors D1-D4 – but the destination of that signal photon appears to be determined by the outcome of its idler-photon twin, 8 nanoseconds later. This would seem to indicate that information on the outcome of the idler photon is travelling backwards in time to dictate the outcome for the entangled signal photon.

The evidence for this is quite compelling: arrival time for each photon at Do and D1-D4 is carefully monitored, with signal photon and idler photon being matched up by that 8-nanosecond difference. Arrival positions at Do are then grouped according to whether the entangled twin registered at D1, D2, D3 or D4. The logic then runs as follows: arrivals at D1 and D2 all occur, in each case, from a mix of R & B sources, so which-path information isn’t available for them; whereas arrivals at D3 and D4 are from B-only and R-only sources respectively – so it’s totally apparent (apparently) which path each of those photons took, i.e. which slot they came through in each case. Accepted wisdom has it that if it’s known which path a photon took then interference will not happen; also, if the path is known to have been through just one slot then this means the photon has changed its form from that of a wave to that of a particle. So a lot is riding on whether or not which-path information has been made available; it completely changes the form and behaviour of the photon (apparently)! This means we’d expect interference patterns to be formed by photons landing on D1 & D2 – and so also their entangled partners landing at Do – but photons landing at D3 & D4, and so also their entangled twins at Do, would not form such patterns.

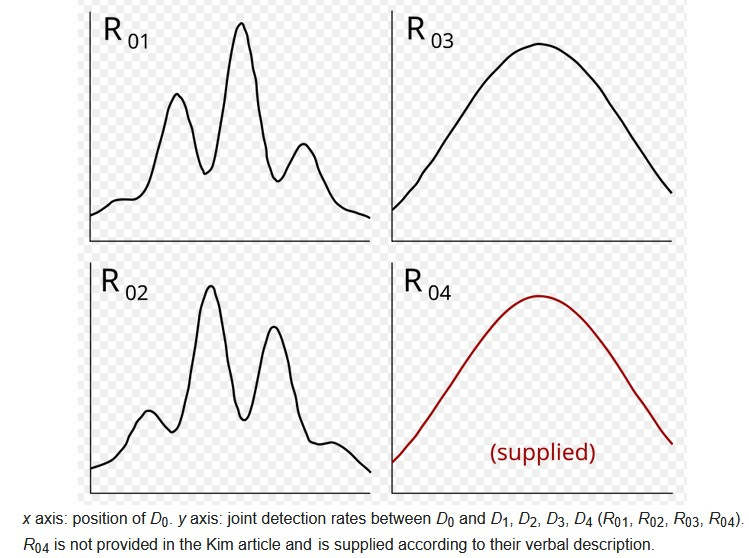
This is (apparently) exactly what happens. Landings at D1 & D2, matched up by synchronised (8ns adjusted) timings with those at Do, each separately show interference patterns at Do when singled out (D1 shows constructive interference, D2 destructive interference, due to that phase difference); whilst landings at D3 & D4, similarly singled out, each show no sign of interference at Do. The distributions of photon ‘hits’ on Do, grouped by coincidence with hits on D1, D2, D3 & D4 respectively, are shown below, demonstrating complementary interference patterns at D1 & D2 but no interference at D3 & D4. Note that the totality of hits on Do (i.e. the sum of these four patterns) shows no sign of interference; the reason for this will be considered shortly. [Author credit: as for schematic of experimental setup above.]

We’re then faced with a major conundrum: landings at Do conform with effects expected at D1-D4, resulting from combining R & B in some cases but not in others; but the decision for each photon, whether to combine R & B or not, is made randomly by beamsplitters after landing has occurred at Do in each case – so how did those photons landing at Do know in each case whether to form part of an interference pattern, or not??? It seems that not only do those photons landing on Do match the outcome for their entangled twins at D1-D4, they do so in each case before the decision has been made as to what that outcome is to be! The only possible interpretation appears to be that photons landing at D1-D4 have sent information back in time to their entangled twin at Do in each case!!

So What’s Going On?!?

A few home truths to start with:

(1) There’s no such thing as wave-particle duality, except in our perception and in our interpretation of events.
Light only ever travels as a wave; its apparent behaviour as a particle is due to (apparent) localisation of its effects, as seen, for example, in the photoelectric effect: the widespread waveform of a high-energy photon registers ‘at one point’ * on that wavefront, at which point all of its energy is transferred to an electron which (with that additional energy) is able to break free of the atom it’s tied to and travel as a free electron. The classic ‘evidence’ of light as a particle, Compton Scattering, is even more evidently wavelike behaviour: see notes at the bottom of this post. The crux of this issue is the fact that ‘particles’ of matter are actually themselves wave-based constructs – a fact not apparent to our physical senses, but now very well established: particle-like behaviour is in fact transfer of energy from one distributed waveform to another. (* So energy transfer is not actually ‘at one point’, it simply appears so in our perception.)

(2) There’s no such thing as ‘which path’: every photon in a 2-slot scenario passes through both slots as a diffracted wave, recombining on the other side (if possible) to produce an interference effect; if the two parts of that ‘split’ wave are kept separate, each part (but not both) has a non-zero probability of registering at some point on its respective wavefront, in which case the part that registers (a probabilistic event) is mistakenly regarded as the path the photon must have taken. The very notion that a photon must have passed through one slot but not the other is patently un-scientific nonsense.

(3) There are no two separate-but-entangled photons; there is one composite waveform energy construct which we, with our limited space-time perception, see as two spatially separated individual entities. That perception is reinforced by the fact that these two ‘separate’ elements of this one construct can pursue different destinies – the joint construct is split, the ‘entanglement’ is broken (in the ‘detection’ situation, as here; other situations, such as re-emission, may retain entanglement). Up to that point the two parts maintain complementary states, complementary parts of the composite energy structure.

So, up to the point that the R & B mix of the signal photon registers with detector Do, that signal photon will have a matching state with its partner idler photon (necessarily, since the two are ‘entangled’, i.e. one composite entity). Since the idler photon’s two strands, R & B, are separated at that time and no interference is possible, the signal photon will likewise not demonstrate any interference – the pattern of photon registration at Do will present as a single peak (in actual practice two closely-spaced peaks, one from R slot and one from B slot – too close together to be separately detectable visibly, as the slots are less than 1mm apart).

The question is: what happens from here on in?

First Things First

Kim et al.’s Delayed-Choice experiment focuses attention first and foremost on the variety of possible outcomes at detectors D1-D4, then relates these back to apparent consequences for matched outcomes at Do (8 nanoseconds earlier in each case). The logic for their conclusions seems very compelling – many might even say irrefutable.

But maybe we should also pay heed to the guidance of the country yokel being asked for directions by a city gent: “If Oi wuz tryin’ to get there, Oi wun’t start from yer”. When looking for an explanation for a puzzling situation, the end-point of that situation is unlikely to prove more fruitful than the starting point. Perhaps we’d do well to begin by considering the starting point, both of this experiment and, equally importantly, of the discovery that first kicked off this whole line of investigation.

Back in 1801, Young showed conclusively that light travels as a wave through both slits in the 2-slit experiment; this has later been proved to apply even for an individual photon. So the R & B components coming out of those two slits, and thence into a pair of entangled lower-frequency photons, both contain elements of the photon wave. So either component in both the signal photon and the idler photon (or a mix of R & B, in two of the four latter cases) has the capacity to register at Do or D1-D4 respectively, with associated probabilities; if the R component registers, say, at D4, this does not show that the photon travelled as a particle specifically through the R slit, it simply shows that probability favoured the wave in the R component when it came to the point of registering. This is not new science, it’s over 220 years old - and it’s no less true today than it was then..

So, moving along the time-line forwards rather than backwards: when R & B components of one photon arrived at Do, the issue of which of those components was the source of registration of the photon is a matter of probabilities, most definitely not of which slot the photon passed through. For the purpose of this analysis it’s 100% irrelevant which component, R or B, proved dominant in the probability stakes and might therefore be considered responsible for delivering that photon. What is of consequence, though, is the position across the screen at which any particular signal photon registered; this gives a clear indication of the phase difference between the R & B components carrying the wave-form for that photon, since that phase difference is determined by the difference in distances between the landing point and the R & B slots respectively.

If we now follow this logic on, along the various paths taken by the idler photon after registration of the signal photon at Do: first, and most crucially, note that the probability amplitudes of each of the components R & B coming out of the prism are equal to the probability amplitudes of the R & B components of the corresponding entangled signal photon which landed at Do; second, the relative magnitudes of those probabilities are defined by the landing position of the signal photon at Do.

Each of those probability components will be split 50/50 by the beamsplitters BSa and BSb respectively – so relative probability of registering at D3 or D4 will likewise depend on the signal photon’s landing point. Likewise BSc will split the remaining probability components for R & B 50/50 in each case before recombining them to land at D1 or D2 – so D1 and D2 will receive the sum and difference of the probability-waves, respectively, corresponding to 25% of each of the R & B components as landed at Do, i.e. in the same proportions as those defined by the landing position at Do.

Now watch the ball closely here. Because this is where the illusion can creep in. Landings at D1, 2, 3 and 4 pick out their time-linked partners at Do, sure – but those partners are not at any time subject to interference constraints.

Registrations at D3 and D4 together comprise 50% of all the idler-photon landings, split evenly between R and B. D3 & D4 landings corresponding to landings at any specific point on Do will be in proportion to the relative B & R ‘probability ratings’ for landing at that point on Do (since this determines the relative amplitudes of wave components arriving at D3 & D4, so hence also the relative probability of registering at each of those detectors, thus picking out the Do landing as a ‘D3 point’ or a ‘D4 point’). This non-interference process will pick out from registrations at Do two smooth humps with slightly different centres, one for each slit – as shown in Fig. 2. This does not require photons passing through a single slot or acting as particles.

The situation with D1 and D2 is slightly more complex (but not a lot). In each case the recombined R & B idler wave components will travel for a further 8 ns after their signal-wave counterparts register at Do, in that same non-interfering pattern as those relating to registrations at D3 and D4 (i.e. as part of that double-hump pattern). Those recombined components will form complementary probability patterns at D1 and D2, through constructive and destructive interference respectively – due to the phase difference of those R & B components at Do and so also at D1 and D2 respectively. This will not show as a visible interference pattern at D1 or D2, but it will create patterns of probabilities defined by interference considerations; those probabilities will cause periodic complementary variations in registrations at D1 and D2 corresponding to 8-ns evolution of the composite waveform which would apply at points across the screen at Do if R & B components at Do had been allowed to interfere with one another. In other words, idler photon registration will vary up-and-down preferentially between D1 and D2 for registration points across the screen at Do – giving exactly the complementary ‘interference profiles’ shown by selection of Do landings by time-matching with registrations at D1 and D2 (which occur on that probability basis).

To sum up:

(a) There is absolutely no interference effect at Do, at any time; any apparent interference effect in subsets of signal photon registrations are solely due to selective picking out of landings at Do synchronised (with 8 ns delay) with idler photon landings at D1 and D2 (N.B. these are coordinated by timings, not by entanglement – there is no quantum entanglement linking idler photons at D1/D2 with signal photons at Do, that was broken at the time of signal photon detection at Do).

(b) Time-based matching of signal photons detected at Do and corresponding idler photons at D3 & D4, respectively, selects out Do landings at any point in proportion to probability amplitudes at D3/D4 – which correspond to the probability amplitudes of B & R at the landing position on the screen at Do; these will be almost equal, with a slight difference due to position relative to the two slits – so this selection process extracts two almost identical non-interference ‘hump’ distributions, with just a slight lateral difference in positions of those two humps corresponding to distance between the two slits.

(c) Similarly, matching of detections at Do and corresponding detections at D1/D2, respectively, selects out Do landings at any point in proportion to probability amplitudes at D1/D2; these are determined by constructive and destructive interference, respectively, between R & B components at D1 and D2 (which are simply 8 ns progressions of each waveform, R & B, at the Do landing point) ; each of these interference effects gives rise to a (different) periodic variation in probability amplitude – so the ratio of these amplitudes will also vary periodically, giving a periodic variation in proportion of registrations at D1 and D2 for successive points across the screen at Do; when these two periodically-varying proportions are linked by timings to landings at all points across the screen at Do, they generate two complementary oscillating landing profiles, similar to interference patterns.

These four patterns can be readily generated by a comparatively simple computer simulation, with no requirement for any signals being sent back in time.

The clear take-home message from this is that:

(1) Far from showing photons behaving as bullet-like particles, the scenario observed in the Kim et al. experiment can only be due to photons acting as waves carrying probabilities;

(2) Far from ever just passing through one slit or travelling along just one path, every photon follows every path, through every slit, to achieve the outcomes demonstrated in that experiment – probabilistically;

(3) This paper’s concluding explicit assertions that “The experimental results demonstrate the possibility of observing both particle-like and wave-like behavior of a light quantum via quantum mechanical entanglement” and “The which-path or both-path information of a quantum can be erased or marked by its entangled twin even after the registration of the quantum” appear to be based more on highly questionable scientific orthodoxy than on objective empirical evidence. The fact that this paper made it through the peer review process into a highly respected journal such as Phys. Rev. Lett. without (apparently) any serious consideration of the probabilistic nature of the processes involved gives serious cause for concern regarding the future of meticulous scientific investigation.

Finally…

The concept of wave-particle duality is deeply ingrained in present-day scientific understanding, first and foremost with respect to light but also with regard to physical matter. The notion of particles of matter exhibiting wave-like behaviour was first proposed by Louis de Broglie in 1924 and demonstrated practically by Davisson & Germer in 1927.

Prior to Young’s experiment, light was generally regarded as being particulate in nature, a view notably advanced by Newton in his corpuscular theory of light; he recognised a wave-like motion in a medium (the aether) through which light was moving, but rejected the notion of light itself being a wave-like effect in that medium – though this did leave several questions hanging for him as to how exactly that worked. When Young demonstrated very clearly that light is a waveform phenomenon, the ‘particle’ concept didn’t go away, as there still seemed to be a lot of evidence in its favour.

In particular the photoelectric effect identified by Einstein (for which he was awarded his Nobel prize) and the Compton Effect (which earned Compton his Nobel award specifically for showing that “electromagnetic radiation could also be described as photon particles following the laws of mechanics”) are considered clear evidence of the ‘particle’ side of wave-particle duality. The former is the basis of the concept of photons, individual packets of energy each carrying a specific payload of energy depending on its frequency: one photon – only if it carries enough energy – can act in a bullet-like way to dislodge an electron from its orbit around an atomic nucleus. The latter shows that a photon can apply principles of conservation of energy and momentum in a manner much like a snooker ball to dislodge, deflect or set in motion an electron whilst itself being deflected with reduced energy and momentum – just like that snooker ball.

First thing to note is that no bullet (snooker ball, etc) extinguishes itself by interacting with another object – whereas a large ocean wave can dissipate itself into nonexistence by dislodging a rock in a coastline. More to the point, an electron has been shown to have wavelike properties: the de Broglie wavelength for a moving particle is inversely proportional to its momentum – directly analogous to electromagnetic waves; it follows that wavelike energy of a photon is re-cast as wavelike energy in a particle through the photoelectric effect.

Even more to the point: no snooker ball reduces its substance by interacting with other matter, whereas this is pretty standard for an electromagnetic wave; in a Compton scattering event a photon is deflected in reduced form, just as is an ocean wave on impacting a rock or a pier support; more than this, the lost energetic substance of a photon in a Compton event becomes part of the energetic substance of the object impacted, as evidenced by the change in de Broglie wavelength of that object. Although cited as proof of the particle-like nature of light, Compton scattering is even more so evidence of its wavelike nature – particularly when one considers interaction between the wavelike form of an electron and the wavelike form of a photon; that interaction is fully explainable in terms of waves.

The notion that a photon can change its state at will between two quite different forms – particularly that it can do so retrospectively (i.e. before coming through those slits) – as a response to being observed or even potentially observed (after coming through those slits) is surely the stuff of unicorns and magic spells rather than carefully considered science. Considered science tells us unequivocally that these two ‘different states’ are actually just two manifestations of one and the same state: the waveform state that light and material particles have in common. The problem lies, not in those two ‘different’ states, but in the inability of ultra-conventional science to come to terms with the fact that matter is composed of waveform energy, configured in a way that our limited perception senses as localised and hence particulate. It’s in the nature of our sensory apparatus to perceive only the ‘core’ or ‘focus’ of each so-called ‘elementary particle’ of matter. Recognition that photons and ‘particles’ of matter are both formed from waveform electromagnetic energy, coupled with the probabilistic nature of interactions between them, eliminates – at a stroke – any hint of an objective difference between light as waves and light as particles.

The Bottom Line

Wave-particle duality of light (and other electromagnetic energy), as an objective 2-state reality, is a myth. The only duality is in the way we choose to observe or measure the effects of light: some observation methods explicitly highlight its true waveform nature; others obscure that nature by focusing on interactions with particles of matter, whilst mis-perceiving them as localised entities and ignoring their waveform nature. This blind spot in scientific thinking is seriously hampering progress in our understanding of, and working with, the physical realm.

Find out more from my other posts, linked and summarised here .

================================================

Be sure to check out Transfinite Mind for a wealth of free resources, including non-technical articles and presentations, as well as books to suit every level of scientific (or non-scientific) background.

Also, if you find these articles interesting and thought-provoking, and you know others who may also find them of interest, please be sure to point those others in this direction. Thanks.

Back with you again soon!