Beyond Einstein: WHY E = mc squared (II)

With High School Maths YOU can know something Einstein didn't know.

[Posts are sequential, to be read/heard in date order - opposite to the order they’re generally displayed in. Paid-for posts have technical content. To see a full list of posts in sequential order, with a brief summary of each, click here . This post isn’t provided in audio form as it depends on various diagrams and a few (fairly straightforward) equations.]

Setting the scene

Almost 120 years ago Einstein stunned the world with a remarkable discovery: the energy contained in any material object is an awesome ninety thousand trillion times its mass (measuring in SI units, the international standard metric system). This has given us the phenomenal output of nuclear power stations and, rather less helpfully, the cataclysmic destructive power of atomic weapons.
What hasn’t been known up to now is why every kilogram of matter, of whatever type, holds enough energy to power the average motor vehicle for hundreds of thousands of years. Einstein didn’t need to figure out why, he just knew that it must be so from his findings on Relativity. But now, with our deeper knowledge of how matter is formed, we can see exactly why this is so.

First we need to understand exactly what mass is. ‘Mass’ actually refers to two properties of a material object:
(a) its resistance to being set in motion, accelerated, or changing direction;
(b) the extent to which it’s attracted by (and attracts) other physical objects.
The former relates to, for example, the mass of a billiard ball, in terms of the energy needed to get it moving at a certain speed: inertial mass. The latter relates to the reading on a set of scales when an object is placed on the scale pan, due to the attraction of gravity: gravitating mass; this is also the measure of the extent to which a large body, such as a planet, attracts other objects under the so-called ‘force of gravity’.

Close inspection, in the light of the cyclic-photon structure of matter, reveals that both of these effects are due to the same property of a material object: its energy content. So by a suitable choice of units these two qualities can be made equal for any given object : its mass.
My peer-reviewed paper Elementary Sub-Atomic Particles: The Earliest Adaptive Systems, published in the leading systems-science journal Kybernetes, shows particle structure to be a stable self-regulating cyclic configuration of electromagnetic energy, cycling on the spot if the particle is static. It responds to input of energy from any external source by shifting to a new cyclic pattern which incorporates a linear component to accomodate that input energy: i.e. the particle adopts a state of motion, most simply viewed as a spiral energy pattern rather than just a circling energy pattern - as shown in the diagram below.
The direction and degree of motion is directly related to the energy input, as well as to the original energy content of the particle itself. In other words, resistance to motion - inertia - can be seen as a particle holding its structural integrity, whilst motion is a particle’s auto-adaptive response to additional energy input, accommodating that extra energy whilst keeping its structural stability by adopting a new stable energy-flow configuration which is constantly flowing into a new position in space. This change of state occurs as a consequence of progressive interference effects between original particle energy and input energy.
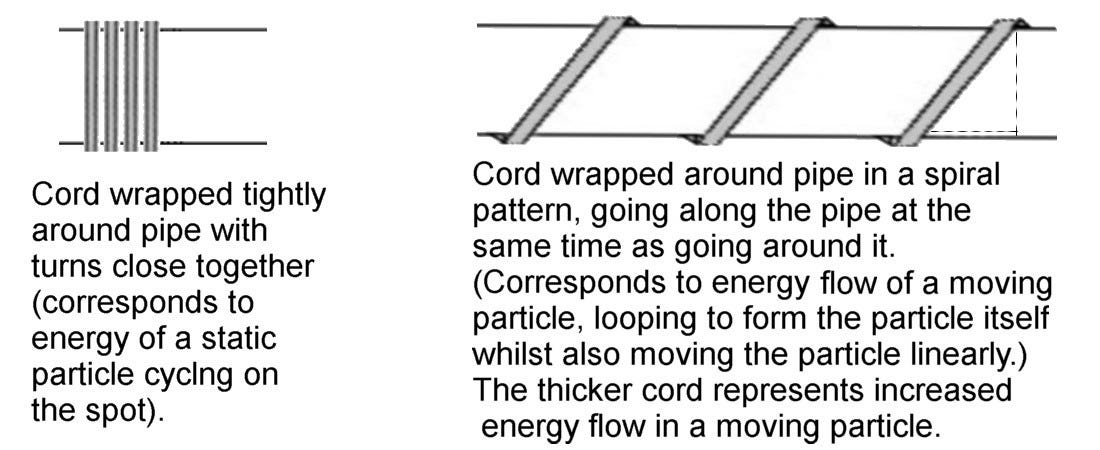
This can be visualised by likening a static particle’s energy-flow to a cord wrapped around a pipe with the turns packed tightly together (all in the same place, in the particle’s case); the moving particle can be likened to that cord being wrapped around the pipe spirally, combining cyclic loops with a linear element: particle structure combined with particle motion. To complete the picture we need to add just one further feature: the cord must be thicker to ensure it doesn’t break, being extended linearly as well as cyclically; this corresponds to the energy input adding to the total energy-flow ‘strength’ (and so maintaining the particle’s structural form) as well as giving it a linear component.

With all this in mind we’re now able to explain the inertial mass of a static object in relation to the energy forming the structure of that object - the E = mc squared of Einstein’s famous mass-energy equivalence relationship.
[Spoiler alert: if you’re looking for some sort of connection between the Higgs boson and this mass-energy equivalence relation, good luck with that! You certainly won’t find it here; this post is concerned with the realities of how a particle’s mass and its formative energy are linked - and the bizarre notion of the Higgs boson doesn’t seem to have anything useful to say about that. A full explanation of the concept of mass has no need of the Higgs-boson concept - it’s utterly irrelevant.]

The energetic structure of a particle in motion is well-defined, consisting of a cyclic energy component, giving the particle its fundamental form, and a linear component moving that form through space. Those two components must be properly balanced to maintain that fundamental form whilst accommodating the linear component as energy of motion; this occurs naturally through self-balancing feedback of electric and magnetic field components in this composite structure.
The primary consideration is that the cyclic energy component will be maintained at a fixed level, to give the particle its fundamental form; as shown above, the additional input energy will introduce a ‘spiral’ element to that particle’s energetic form, moving it linearly through space at the same time as the looping component maintains its structure.
One further consideration which will help us to pin down this mass-energy relation, showing its precise causation (not identified by Einstein), is the constant speed of this structural energy: c, the speed of light. This is the speed of both the formative energy flow in the static particle and the composite energy flow in the moving particle; this means of course that the formative-energy component in the moving particle will be at a reduced speed, since it combines with the motion-energy component (which is of course at the same speed, v, as the particle’s own speed) to give the composite energy flow speed, c. [Note that this also explains the phenomenon of relativistic time dilation, as explained in detail in the post Time dilation in complex energy-flow structures.] This speed, and so also (implicitly) the mass of the particle, is defined by the self-regulating electromagnetic feedback process that ensures the structural stability of the particle.

Time for a few diagrams

First let’s look at a diagram showing the energy components of a moving particle. The vertical side of this triangle represents the cyclic energy forming the basic structure of the particle; the length of this side will always be the same, whatever the speed of the particle, since the same amount of energy will always be required just to hold the particle together. This side corresponds to the vertical lines of cord in the first diagram above, representing the formative energy of a static particle; it also corresponds to the dotted vertical line on the diagonal cord, showing the cyclic component of the spiral energy flow this cord represents.

The diagonal side in this triangle represents the full energy flow forming a moving particle, corresponding to the diagonal cord in the diagram above. This full energy flow consists of the original formative energy of the static particle plus the additional energy input to give the particle motion.
[The horizontal side represents the linear-motion energy component, corresponding to the horizontal dotted line in the above pipe diagram. For those familiar with the energy-momentum relation, this is the element pc - particle momentum x light speed.]

Now we need to relate that diagram to energy input into a particle of a certain mass to achieve a particular speed. This is complicated slightly by the fact that any object’s effective mass - its resistance to acceleration - increases as its speed increases (because its total energy content increases). We can get over this, though, by considering only a very low speed compared to the speed of light - say 0.001c (one thousandth of light speed) - in which case our calculations will be accurate to better than one part in a trillion.
If we now consider a force F which accelerates our particle from static to speed 0.001c in one second, that acceleration is of course 0.001c per second. Using Newton’s 2nd law of motion, force = mass x acceleration, we get that F = m x 0.001c (we’re taking the mass m of our particle as constant - that’s our approximation).
Since the particle accelerates uniformly from 0 to 0.001c over 1 second, its average speed over that second is halfway between 0 and 0.001c - and that average speed for a time of 1 second gives a distance: 1/2 of 0.001c metres (since c is measured in metres per second).
So if we now apply the standard principle that energy input = force x distance, we get that the energy input to our particle is F x 1/2 of 0.001c.
Replacing that F with m x 0.001c (from our Newton’s 2nd law result), we get that the energy input to our particle to give it motion is: m x 0.001c x 1/2 of 0.001c. This can be written more tidily as: 1/2m x (0.001c)^2 [^2 simply means ‘squared’.]
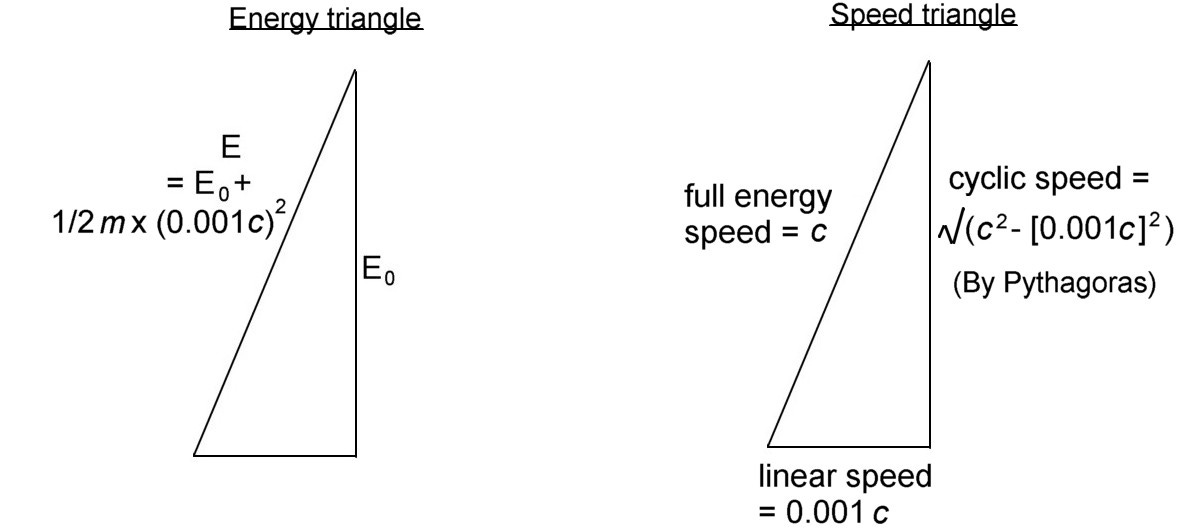
So that Ek, the kinetic energy in our triangle above, is equal to: 1/2m x (0.001c)^2
[Note that this corresponds to Newton’s formula for kinetic energy: 1/2 mv^2 .]

Time now for a couple more triangles.
The first of these triangles is the same energy triangle as we have above, except that we’ve now put in a value for the kinetic energy in terms of particle mass m.
The second triangle shows the components of speed of that energy flow, cyclically and linearly in the direction of particle motion. That linear energy-flow speed is of course the speed of the particle itself, 0.001c, and the overall energy speed (diagonal side) is c, the speed of light, since it’s the light-flow that’s forming the moving particle.

Ok, so we’ve established that the inertial mass of a particle (or any object) is simply a result of its requirement for structural stability. Now these two triangles can show us exactly how that requirement determines the value of that inertial mass m in terms of the particle’s (or object’s) formative energy content.

The first thing to notice is that these two triangles must be the same shape - the mathematical term is similar. This must be so because the velocity of each component of the energy flow - cyclic, linear, overall flow - must be in the same direction in each case as those energy-flow components themselves.
From this it follows that the diagonal side divided by the vertical side is the same for each triangle - the proportions of one triangle match those of the other.

The first thing to note is that the two approximations used in this calculation effectively cancel each other out to make this result totally accurate (not just ‘better than one in a trillion’).
The second is that this result holds for every speed of a particle, not just when static: the increase in total particle energy at any speed is precisely balanced by the increase in effective mass - or to put it more accurately, the effective mass rises precisely in line with the total energy.
Both these points are established in detail in the post: The Maths of Mass-Energy Equivalence, which uses (Newtonian) calculus and Newton’s laws of motion to derive this result - no Relativity required. [You can actually check that first point yourself quite easily; just follow the simple steps under ‘Confirmation’ below.]

The third thing to note is that inertia, and inertial mass, are direct consequences of the energy content of a particle and the way in which that energy content increases with states of motion to maintain the particle’s structural integrity - no Higgs boson or Higgs field required, either.

Confirmation
(of the exact result)

The result we derived above was based on two approximations (both very accurate, to better than one in a trillion). We can make this exact, eliminating those two approximations, very simply as follows:
We envisaged the particle speed increasing from zero to one thousandth of the speed of light, 0.001c. That term, 0.001c, cancelled out and doesn’t appear in the final result - but it was that small speed which introduced a tiny variation from the exact results in two places.
If instead we envisage an even smaller speed, say one millionth of the speed of light, 0.000001c, instead of one thousandth, that gives far, far smaller variations in those two approximations - but makes absolutely no difference to our final result (since that speed term cancels out). So in that case our two slight variations are far, far closer to the true result - to within trillionths of trillionths.
We can take this idea as far as we like, to when the speed reached in one second is only an infinitesimal fraction of the speed of light - effectively zero. At that point the variations from the true situation (in our calculations) are also effectively zero - the results of our calculations are totally precise, our formula is 100% correct.
The point is, our calculations in this post don’t rely on any particular speed for their validity, only that we consider acceleration from zero to some nominal speed. We can make that nominal speed as small as we like. This is the principle used in Newton’s (and Leibniz’s) mathematics of infinitesimals or calculus: as we make our nominal speed smaller and smaller, it becomes clearer and clearer that the structural energy of any particle is, quite precisely, its mass multiplied by the square of the speed of light:

Einstein figured this must be so, from his findings on Relativity. But neither he nor those who came after him knew what it was that caused this to be so. The key to understanding this relationship is the fact that an object’s mass is a measure which determines the amount of additional energy required by the object to achieve a particular (increase in) speed whilst maintaining its structural integrity; this is in turn determined by the object’s formative structural-energy content.
In other words, it’s mass which is dependent on energy content, not vice versa.
[That same energy content determines an object’s gravitational effect on other objects, and so also its gravitational mass. So it is that, with a suitable choice of units, any object’s gravitational mass is equal to its inertial mass. This is made very clear in the earlier post: Gravitation: What's the Big Attraction?]

Next up

Next up: Disentangling Quantum Entanglement: It’s time to get real about Nonlocal Realism.
In the meantime, be sure to check out Transfinite Mind for a wealth of free resources, including non-technical articles and presentations, as well as books to suit every level of scientific (or non-scientific) background.
Also, if you find these articles interesting and thought-provoking, and you know others who may also find them of interest, please be sure to point those others in this direction. Thanks.

Back with you again pretty soon!